Οι διαστάσεις των Χαρτιών κατά ISO 216
Τα στάνταρ μεγέθη των χαρτιών, προσδιορίζονται και περιγράφονται από τo ISO 216.
Εκεί αναλύονται με σαφήνεια όλες οι διεθνώς στάνταρ διαστάσεις χαρτιών, όπως π.χ. το Α4, που ισχύουν στις περισσότερες χώρες του κόσμου.
Το ISO 216 κυκλοφόρησε για πρώτη φορά το 1975 και βασίζεται στο Γερμανικό DIN 476 που υπάρχει από το 1922. Έκτοτε, αναθεωρείται, όπως έχουν υποχρέωση όλα τα Στάνταρ,
κάθε πέντε χρόνια. Σήμερα το τρέχων Στάνταρ, είναι το ISO 216:2007.
Στο ISO 216 περιγράφονται δύο σειρές μεγεθών.
Η Σειρά Α και η Σειρά Β. Στο ISO 269, που κυκλοφόρησε το 1985, ορίζεται και η
Σειρά C για φακέλους.
Περιληπτικά, οι διαστάσεις των πλευρών του μεγέθους Α έχουν έναν λόγο μεταξύ τους, ο οποίος είναι:
√ 2 ≈ 1,414.
Έτσι λοιπόν με δεδομένο αυτό το λόγο (1:1,414) και για το εμβαδόν ενός τετραγωνικού μέτρου, όπως θα δούμε παρακάτω, ορίζεται το σχήμα Α0 με πλευρές:
841Χ1189 χιλ. και κόβοντας πάντα την μεγάλη διάσταση στην μέση, παίρνουμε διαδοχικά τα σχήματα Α1, Α2, Α3, Α4 κ.ο.κ.
Βασικές Αρχές (κανονικά προερχόμενα μεγέθη)
Αυτό το σύστημα μεγεθών χαρτιού είναι σχεδιασμένο στην ακόλουθη βάση: κάθε κανονική σειρά (κανονικώς προερχόμενα μεγέθη) αποτελείται
από μια σειρά μεγεθών που σχηματίζονται με τέτοιο τρόπο ώστε κάθε μέγεθος να επιτυγχάνεται με διαίρεση του αμέσως μεγαλύτερου μεγέθους
σε δύο ίσα μέρη, με τη διαίρεση να είναι παράλληλη πάντα στην κοντύτερη πλευρά (η αρχή του μισού, δηλ. το δίπλωμα ή το κόψιμο του χαρτιού στην
μέση, γίνεται στην μέση της μεγαλύτερης πλευράς). Κατά συνέπεια, τα εμβαδά δύο διαδοχικών μεγεθών έχουν αναλογία 2:1.
Όλα τα μεγέθη σε κάθε σειρά είναι γεωμετρικά όμοια μεταξύ τους (η αρχή της ομοιότητας).
Αυτή η απαίτηση, σε συνδυασμό με αυτήν που εξηγήθηκε στην προηγούμενη παράγραφο, δίνει την ακόλουθη εξίσωση για
πλευρές x και y ενός δεδομένου μεγέθους:
y : x = 2 : 1 = 1,414. (1)
Με άλλα λόγια, η αναλογία μεταξύ των πλευρών x και y είναι ίση με την αναλογία μεταξύ της πλευράς και της διαγωνίου ενός
τετράγωνου.
Το βασικό μέγεθος της σειράς Α (Α0) έχει επιφάνεια 1 m2. Επομένως ισχύει η ακόλουθη εξίσωση:
x * y = 1 m2 (2)
Οι εξισώσεις (1) και (2) δίνουν τα ακόλουθα μήκη των πλευρών για το βασικό μέγεθος της σειράς Α:
x = 0,841m και y = 1,189m
Η κύρια σειρά μεγεθών επιτυγχάνεται λαμβάνοντας το βασικό μέγεθος που περιγράφηκε και εφαρμόζοντας τις αρχές που περιγράφηκαν παραπάνω.
Αυτή η σειρά μεγεθών, ονομάζεται σειρά ISO-A.
Τις διαστάσεις χαρτιών της σειράς Α, Β και C, μπορείτε να τις δείτε στον πίνακα που ακολουθεί.
| # |
Σειρά A |
Σειρά B |
Σειρά C |
| Μέγεθος |
χιλ. |
χιλ. |
χιλ. |
| 0 |
841 × 1189 |
1000 × 1414 |
917 × 1297 |
| 0+ |
914 × 1292 |
1118 × 1580 |
- × - |
| 1 |
594 × 841 |
707 × 1000 |
648 × 917 |
| 1+ |
609 × 914 |
- × - |
- × - |
| 2 |
420 × 594 |
500 × 707 |
458 × 648 |
| 3 |
297 × 420 |
353 × 500 |
324 × 458 |
| 3+ |
329 × 483 |
- × - |
- × - |
| 4 |
210 × 297 |
250 × 353 |
229 × 324 |
| 5 |
148 × 210 |
176 × 250 |
162 × 229 |
| 6 |
105 × 148 |
125 × 176 |
114 × 162 |
| 7 |
74 × 105 |
88 × 125 |
81 × 114 |
| 8 |
52 × 74 |
62 × 88 |
57 × 81 |
| 9 |
37 × 52 |
44 × 62 |
40 × 57 |
| 10 |
26 × 37 |
31 × 44 |
28 × 40 |
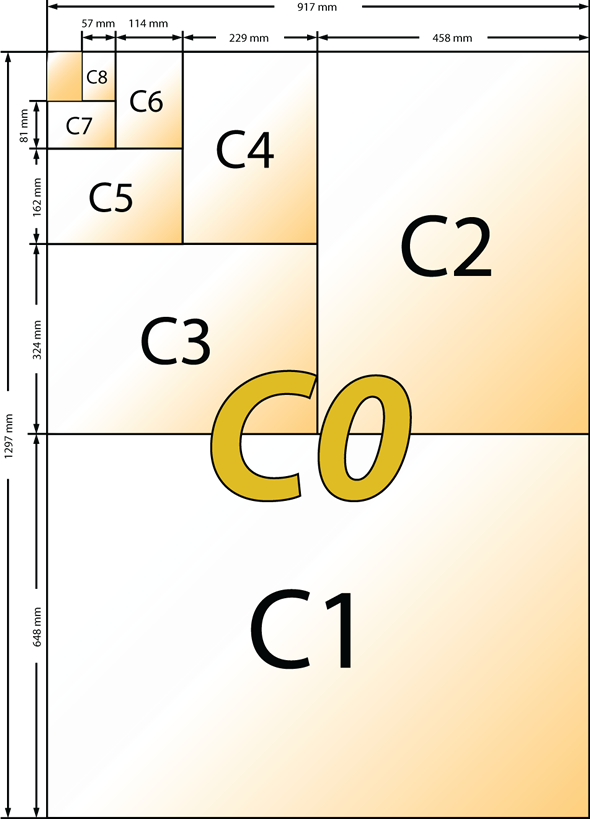
Σχηματική παράσταση Διάστασης Χαρτιού ISO A
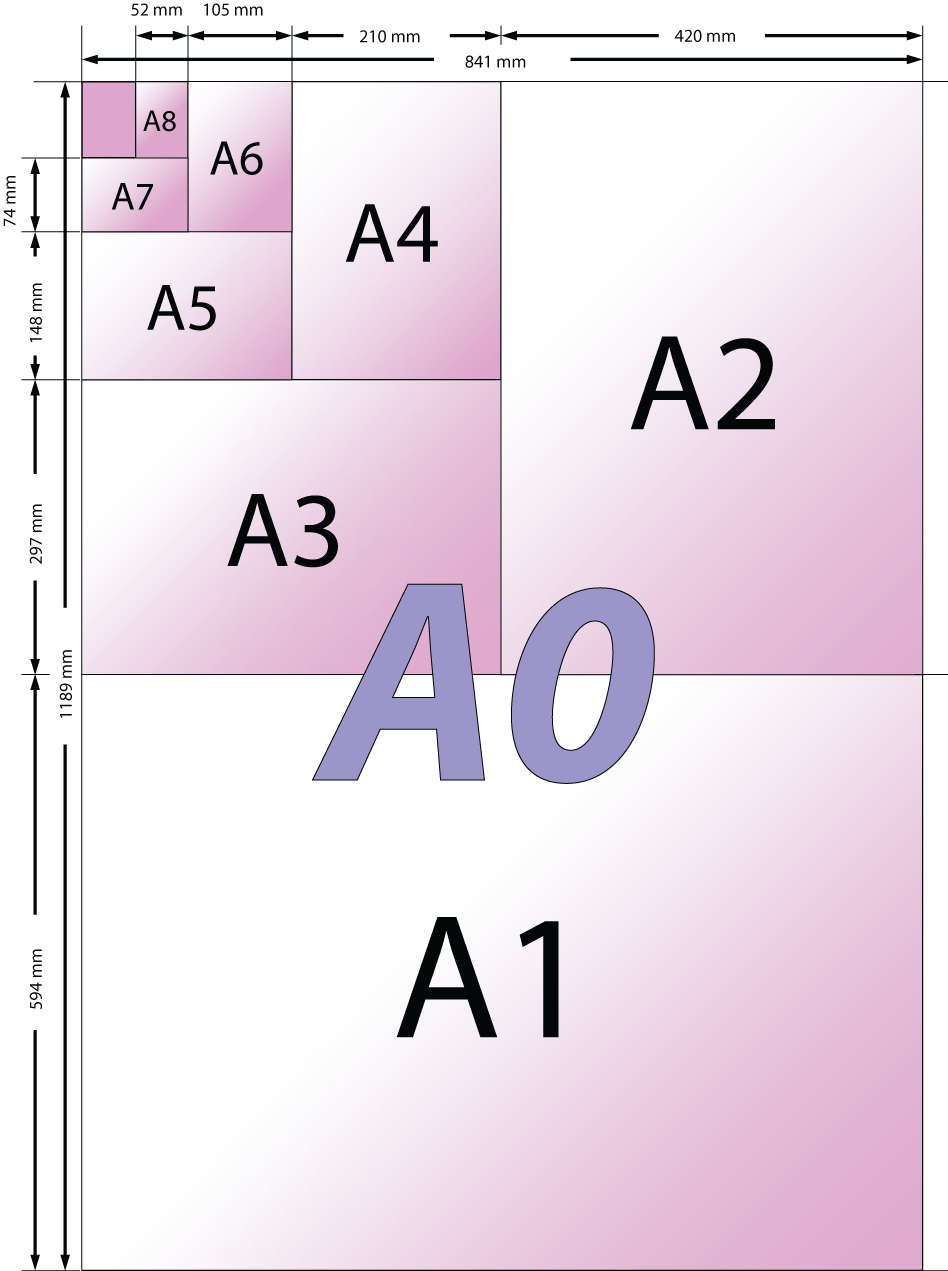
Σχηματική παράσταση Διάστασης Χαρτιού ISO B
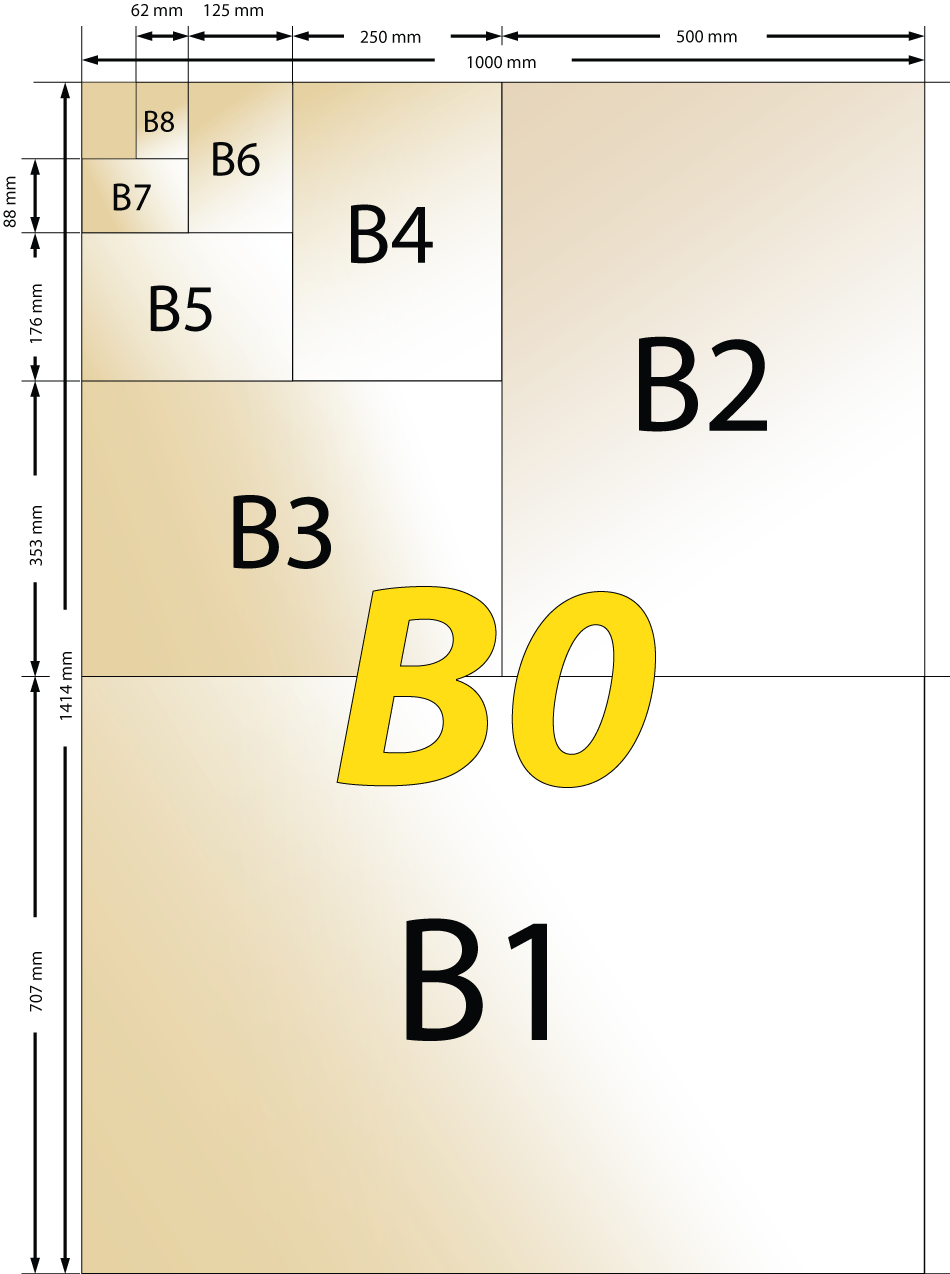
Σχηματική παράσταση Διάστασης Χαρτιού ISO C